- São Paulo - SP
- Quem Somos FAQ Fale Conosco Cadastre-se Login
[Imagem: Tumisu/Pixabay]
Previsão de terremotos
Quando se fala em prever terremotos, talvez você pense em sismógrafos mais avançados, em grandes redes de sensores monitorando os primeiros sinais dos tremores, ou talvez até em grandes projetos de perfuração para monitorar a Terra desde suas entranhas.
Mas o maior avanço na previsão de terremotos em muitas décadas, alcançado agora por Takayuki Nagata e colegas da Universidade de Tohoku, no Japão, não dependerá de nenhum sensor adicional e nem mesmo de um único centímetro de perfuração.
A inovação é puramente matemática, envolvendo um novo método de análise dos dados já coletados em todo o mundo - o novo método mostra ondas sísmicas "escondidas" nos dados porque os métodos de análise atuais não as detectam.
Nagata conseguiu vencer os desafios matemáticos da análise convencional de "matriz espectral", uma técnica usada para analisar sinais sísmicos de três componentes. Ao introduzir componentes de retardo de tempo, o pesquisador conseguiu caracterizar diversas ondas polarizadas, detectando eventos sísmicos que passam despercebidos pelos métodos convencionais.
Além da detecção de terremotos, esta inovação matemática abre caminho para melhorar uma variedade de aplicações, já que o espectro de uma matriz é utilizado em uma larga variedade de situações, das buscas feitas pela internet às análises geofísicas feitas em busca de novos depósitos minerais.
Espectro de uma matriz
A coleta de dados sísmicos depende do número e do posicionamento de sensores chamados sismômetros. Como a implantação desses sensores sísmicos é sempre limitada por área, a otimização da extração de dados de cada sensor é crucial. Um método promissor para fazer isso é chamado análise de polarização, que envolve o estudo do movimento de partículas em um espaço 3D.
Ele é promissor porque permite aproveitar dados de três componentes, oferecendo mais informações do que dados de um componente. Esta abordagem permite a detecção e identificação de várias formas de ondas sísmicas polarizadas, incluindo ondas S, ondas P e outras.
A análise de polarização utilizando uma matriz espectral, em particular, é uma técnica utilizada para analisar a forma como as partículas se movem em trêsdimensões ao longo do tempo e em diferentes frequências, ou seja, no domínio tempo-frequência. No entanto, em cenários onde o sinal é fraco em comparação com o ruído de fundo - conhecidos como eventos de baixa relação sinal-ruído - a análise do espectro da matriz tem suas limitações: Devido a restrições matemáticas, ela só consegue caracterizar o movimento linear das partículas (ou seja, as ondas P de movimento rápido e fáceis de detectar), ficando cega a outras formas de onda (como as ondas S secundárias).
"Nós superamos os desafios técnicos da análise da matriz espectral convencional e a expandimos para uma realização mais ampla de polarização, introduzindo componentes de retardo de tempo," disse Yusuke Mukuhira, membro da equipe.
|
|
A incorporação de componentes de retardo de tempo não apenas permitiu a caracterização de várias ondas polarizadas, incluindo as ondas S, como permitiu a detecção de eventos de baixa relação sinal-ruído com amplitudes menores.
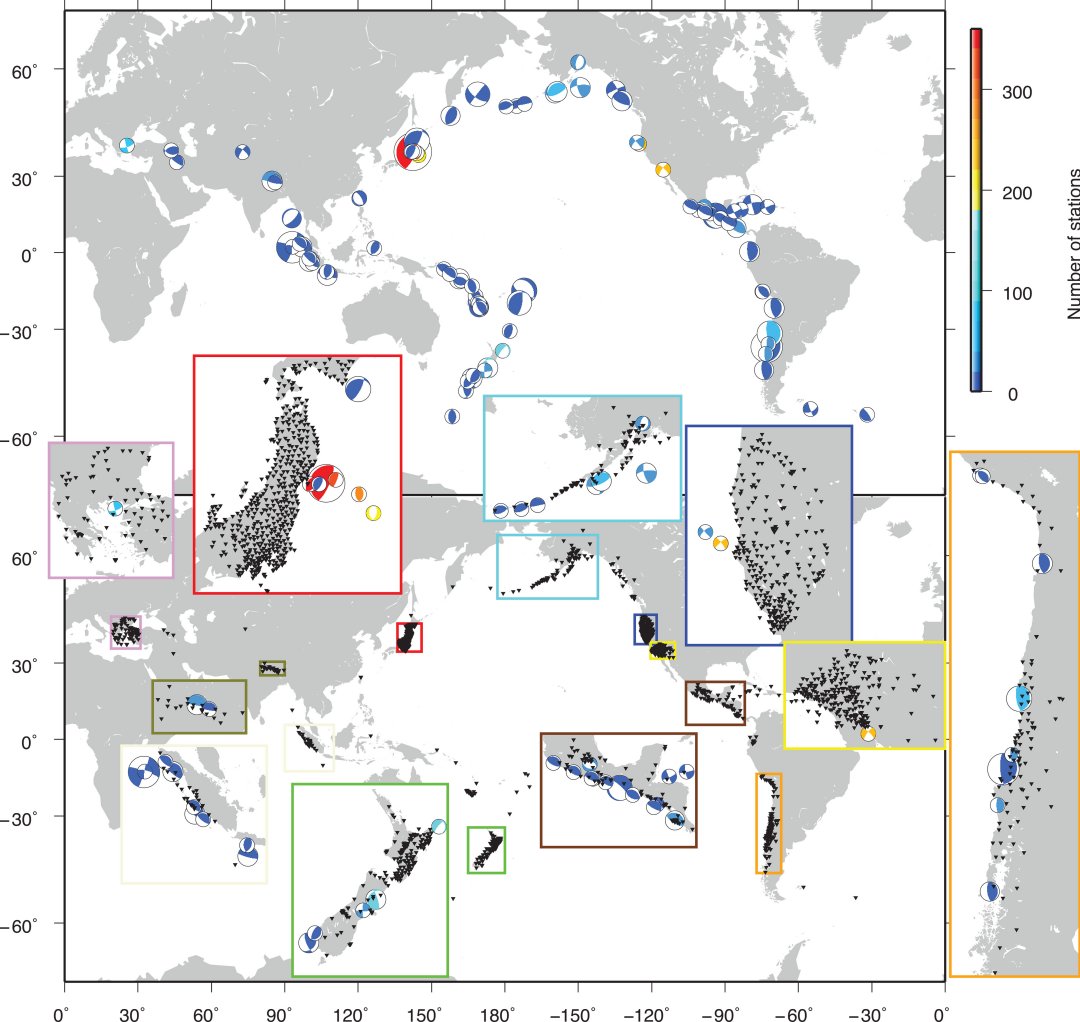 |
Autovetor
Uma inovação chave alcançada pela equipe consistiu na introdução de uma nova função de ponderação baseada nas informações de fase do primeiro autovetor - um vetor especial que, quando multiplicado pela matriz, resulta em uma versão em escala do vetor original.
O objetivo da função de ponderação é atribuir diferentes níveis de importância a diferentes partes dos sinais, reduzindo assim os alarmes falsos. Testes de formas de onda sintéticas mostraram que esta adição melhorou significativamente a avaliação da polarização das ondas sísmicas, um fator crucial para distinguir o sinal do ruído.
A equipe validou sua metodologia utilizando dados do mundo real registrados no campo de gás de Groningen, nos Países Baixos. Os resultados demonstraram um desempenho superior de detecção de movimento sísmico, trazendo à luz dois eventos de baixa relação sinal-ruído que haviam passado despercebidos pelos métodos convencionais.
Bibliografia:
Artigo: Polarization Analysis in Time-Frequency Domain by Complex Spectral Matrix: Application to Various Phases of Seismogram
Autores: Takayuki Nagata, Yusuke Mukuhira, Jingyi Sun, Hirokazu Moriya, Takahiro Shiina, Taku Nonomura
Revista: IEEE Transactions on Geoscience and Remote Sensing
DOI: 10.1109/TGRS.2024.3352817



